Fragment och hågkomster ur ett lärarliv

"…Ty den som vid befordran till en skoltjenst tänker: Kära själ! Nu har du bröd, ät och drick och gör dig goda dagar - den är en lågsinnad menniska som aldrig fattat betydelsen af sitt kall, och som förgäter att han en gång måste avlägga räkenskap för hvarje honom anförtrodd barnasjäl". Citatet hämtat ur O E L Dahms Skolmästarkonst utgiven 1846.

En mulen novemberdag 1980 vid Sävar skola, 18 km norr om Umeå, slog en elevs kommentar ned som en blixt i mitt sinne. Rätt självklart, men då först blev det uppenbart för mig hur viktigt det är att använda språket i matematik. Språket är ju faktiskt bärare av all mänsklig kunskap. Sedan dess har jag arbetat med ”Språkutvecklande matematik” som för mig har sin grund i den utbildning jag fick vid folkskoleseminariet i Umeå på 60-talet. Webbsidan WebMath visar hur jag gjort verklighet av mina tankar om ”Språkutvecklande matematik” . Klicka här för att se ett exempel

29 maj 1965 tog jag, Fredrik Westman, folkskollärarexamen vid Umeå folkskoleseminarium. 14 juni 2007 gick jag i pension efter 42 år som lärare. Det har varit en resa fylld med hårt jobb, glädje och många tillfredsställande ögonblick då jag sett att jag verkligen gjort skillnad för eleven. Men det har också varit smärtsamt att uppleva all den förnedring som läraryrket och skolan fått utstå. Modernitetens förkastelsedomar över beprövad pedagogik lämnade fältet helt öppet för stor glömska, förvirring och absurditeter. De officiella påbuden sammanföll med idéerna som låg i tiden. Men det vid skrivbordet uttänkta bortsåg från människan sådan hon är och moderniteterna fungerade därför mycket dåligt i skolans verklighet.

Det verkar generellt vara så att kunskapen i ett samhälle, det kollektiva medvetandet, lär sig ett och samtidigt glömmer ett annat. Hur kan det t ex annars vara möjligt att nazister åter vandrar på våra gator?

Eftersom majoriteten av de lärare, skolledare och myndighetspersoner som nu är verksamma är uppfödda med den pedagogik/didaktik som svepte in i skolan och raderade ut mycket gott av den ”gamla” beprövade pedagogiken tänkte jag att det kanske skulle kunna vara av intresse att ta del av de bakomliggande tankar, i form av konkreta exempel, och som finns invävda i WebMath, tankar som bygger på den väl beprövade pedagogiken. Fast - kan det för dagens skolpersonal överhuvud taget vara intressant att läsa om vad som hände i skolan från 60-talet och framåt. Givetvis kan det kännas som om fragmenten och hågkomsterna är hämtade ur stenåldern. Men om man betänker vad prof Jonas Linderoht skrev i DN Debatt 24 aug 2016 ”Jag ber om ursäkt för 90-talets pedagogiska idéer”, borde det finnas ett och annat användbart tips att hämta ur den pedagogik som rådde innan de stora omvälvningarna som slog rot på 70-talet, tog fart på 80-talet och blommade ut på 90-talet.

Mina fragment och hågkomster kommer knappast att komma i kronologisk ordning, möjligtvis de första av mina inlägg. Allteftersom det dyker upp minnen publicerar jag dem. De kommer antagligen att vara av två slag, dels själva lärarrollen och lärarens roll i samhället, dels konkreta exempel på den pedagogik jag använt.

1. När börjar ett då lärarliv?

Det finns säkert lika många svar på den frågan som det finns lärare. För min del började mitt lärarliv på vår bondgård i Uttersjöbäcken, ca 4,5 mil sydost om Skellefteå. Vår griskulting blev min första elev. Han led av bensjuka och det ansågs att kultingen behövde vara utomhus för att få motion och kunna böka i jord och sand. Jag var i 7-årsåldern och blev utsedd att övervaka grisen så att den inte sprang till skogs. Vi blev bästa kompisar, och jag märkte snart hur läraktig han var. Det dröjde inte länge innan han glatt grymtande och med knorr på svansen följde mig som en hund då vi tog promenader. Jag märkte också att knorren var viktigt för att inlärandet skulle fungera. En lärdom som jag tagit med mej in i lärarlivet. En harmonisk elev med knorr på svansen är en förutsättning för bra inlärning.

Inne vårt kök trivdes kultingen inte alls. De små klövarna halkade på den glatta fernissade 50-talskorkmattan, ungefär som i filmen där Bambi halkar omkring på isen. Däremot trivdes grisen utmärkt då jag tog honom med tvärs över landsvägen till vårt hallonställe. Medan jag plockade hallon bökade han förnöjt runt i riset och ofta glömde jag locka med honom då jag återvände. Då var det bara att ropa på honom och han kom som skjuten ur en kanon. Fast en gång höll det på att gå illa. Samtidigt som grisen skulle korsa vägen kom folkskollärarinnan Agda Forsman cyklandes i god fart. Krocken såg oundviklig ut, men "kanonkulan" passerade några centimeter framför framhjulet och jag minns hur Agda förskräckt ropade, "Men herre gud, en gris!".

Sommarlovet tog slut och mitt umgänge med kultingen som växte ut till en fullstor gris blev alltmera sporadiskt. Han vistades hela tiden i kätten. Men jag hade fått smak på pedagogik med djur. Av någon anledningen som jag inte minns blev mitt nästa projekt att hypnotisera kor. Nån timme efter att korna var mjökade och fått sina givor hö blandat med melass (en slags sirap) gjorde jag min insats. Jag smög mig osedd in till korna. Det rådde en harmonisk stämning. Det var helt tyst. Det enda som hördes var kornas idisslande och rapet då de stötte upp nästa boll från vommen. Tänk om alla elever vore både mätta och harmoniska och klassrumssituationen andades samma harmoni. Det vore optimal förutsättning för pedagogik. Jag tog fram en mjölkpall som jag ställde mig på och började sakta veva runt med utsträckt arm. Snart började korna följa armen med blicken och efter ytterligare en stund rullade korna sina huvud i takt med min svängande arm. Jag stannade armen tvärt och höll den blixtstilla. Kornas huvuden "frös fast" och stirrade hypnotiskt på armen. Total koncentration. Så hoppade jag till lite och sa buh. Hypnosen försvann och "hela havet stormar" bröt loss - för en kort stund. Sedan återgick allt till harmoni igen och jag smög mig nöjd in för att äta kvällsgröten. Jag berättade aldrig för någon om mina pedagogiska övningar. Det kändes som en allt för udda hobby. Antagligen hade jag blivit förbjuden att hypnotisera kor.

Det var så mitt lärarliv började. Sedan blev jag simlärare i Lövångers kommun och så småningom folkskollärare och senare ämneslärare i matematik, fysik och kemi, och numera mattelärare via webben.

2. Blixten - ”Å de va´ fan så högt gräs!”

En novemberdag 1980 vid Sävar skola. Det var då blixten slog ned i mitt sinne. Minnesbilden är fortfarande tydlig och detaljerad efter så många år. Björn satt längst bak i klassrummet, lite till höger räknat från katedern. Då jag lyfte blicken kunde jag genom klassrumsfönstret skymta de avlövade alarna nere vid Sävarån. Det var en mulen dimmig novemberdag. Jag hade haft en genomgång om hur man beräknar arean av en rektangel och kvadrat. I stället för, som det stod i boken, bas och höjd, använde jag begreppen längd och bredd. Då eleverna, efter genomgången, arbetat några minuter med uppgifterna i boken ropade Björn på mig. ”Kolla här” och så läste han uppgiften högt för mig. ”Beräkna arean av en gräsmatta med basen 40 meter och höjden 20 meter”. Björn tittade upp, ”Å de va fan så högt gräs”! Det var då blixten slog ner i mitt sinne.

Vilka bilder och begrepp får våra elever av det som förmedlas via läroböcker och vår undervisning? Det var den fråga som jag intensivt började grunna över. Vilket språk, vilka ord, vilka bilder förmedlade jag då jag skulle introducera ett nytt matematiskt begrepp? Och hur tänker eleverna – egentligen? Under mitt ältande av dessa frågor upptäckte jag hur märklig talbild jag har. Talslingan som Hiam, (Kolla här) i WebMath beskriver, är just min talbild i förenklad och förkortad form. Jag har aldrig haft problem med matematik. Däremot har huvudräkning fungerat dåligt, därför att i min talbild finns inga genvägar, bara att vandra framåt eller bakåt i talslingan. 77 – 39 är t ex problematiskt om svaret ska fram snabbt. Då låser det sig och jag börjar vandra i talslingan i ställt för att t ex räkna 78 – 40 = 38. Då jag började skolan var inte huvudräkning så viktigt, det viktiga var att räkna fram rätt svar. Jag fick leva i min bildvärld och använda algoritmer och jag har aldrig haft problem att anpassa min talbild till decimalsystemet, tallinjen m m. Kolla intervjun.

Under mitt ältande av hur jag tänker tal upptäckte jag också att jag har en bildslinga för veckan, en nästan cirkulär bildslinga för året och en bildslinga för tidslinjen. Jag är född 1942. Från 1942 till dags dato slingrar sig min tidslinje fram med bl a tvära svängar vid 1950 och 1960. Jag ser varje år som en tydlig fast punkt på linjen. Om jag tittar ”bakåt” på tidsslingan svänger den tvärt vid 1940 och blir sedan suddig.

På alla föreläsningar som jag hade runt om i Sverige på 80- och 90-talet tog jag alltid upp frågan ”Hur tänker du – egentligen?” Jag fick mej till livs de mest märkliga sätt att tänka tal, veckan, året och tidslinjen. Den insikt jag fick av alla ”vittnesbörden” var att det framför allt handlar om att vi alla har vårt personliga, optimala sätt att lära in – inbilda och att språket är bärare av all mänsklig kunskap. För att verkligt lyckas med utlärning - utbildning - måste man alltså med språkets hjälp på ett variationsrikt sätt förmedla bilder så att eleverna får möjligheten att inbilda på sitt optimala sätt. Min pedagogiska ledstjärna har sedan dess varit: "Ju flera sinnen man får använda desto bättre blir inlärningen". Detta självklara faktum glöms tyvärr sakta men säkert bort ju högre upp i klasserna eleven kommer.

3. Språket - bärare av all mänsklig kunskap.

Språket är bärare av all mänsklig kunskap. Språk kan vara det talade och skrivna ordet, men även bilder, animationer, musik mm. Min ledstjärna i arbetet med WebMath har varit att med hjälp av den digitala tekniken visa kärnan i den beprövade, men bortglömda, pedagogiken då det gäller undervisning i matematik. Jag tror absolut inte att den digitala läraren kan ersätta den analoga läraren. Däremot tror jag att den digitala läraren kan var ett bra komplement, men - den stora frågan är vad som får eleven att lyssna och försöka själv?

Det är numera ytterst få som känner till att en ansökan 1962 till folkskollärarseminarier i Sverige gjordes i två steg. Först en grovsållning med hjälp av den sökandes betyg för att avgöra om hen hade tillräckligt djupa kunskaper. Därefter följde två dagars lämplighetstester, där bl a stor vikt lades vid den sökandes förmåga att livfullt kunna berätta och beskriva utifrån ett givet ämne, och att kunna skapa ”Det goda samtalet” i klassrummet. Det låg en stor visdom i detta. Det är ju det som är den utmaning man möter som lärare, d v s att med hjälp av samtal, berättande, visande och instruerande kunna inspirera eleven att både vilja lära och att försöka själv - och att ställa krav på eleven. En annan intressant aspekt var att det i varje klass vid folkskoleseminarier runt om i Sverige skulle var 50% kvinnor och 50% män.

På 70-talet började "den samtalande, berättande, visande och instruerande läraren” anses förlegad, och den gamla svenska skolkulturen raserades i allt snabbare takt. Jag har upplevt den svenska skolans förändring personligen och tillhör den grupp lärare som sedan 70-talet hade ”fel" åsikt och använde ”förlegade" metoder. Vi var många som stretade emot, men metoderna ”Gör så här så får du rätt svar” och ”Eget arbete” stämde in på tidsandan och gick inte att stoppa. De youtubefilmer som nu översvämmar Internet visar hur djupt förankrad ”Gör så här”-pedgogiken är. Filmerna berättar ”hur man gör” utan att resonera och diskutera omkring vad det matematiska begreppet är – egentligen. Filmerna är en återspegling av denna "härmapedagogik". Det pedagogiska/didaktiska förfallet är djupt tragiskt. Att sedan professor Jonas Linderoth i DN Debatt ber om ursäkt känns enbart hånfullt och okunnigt. På 90-talet fullföljdes bara det som drogs igång på 70-talet.

I grunden handlar detta om att riksdagen 11 mars 1971 fattade beslutet om tjänstepliktslagen då lärare tvingades tillbaka från den pågående konflikten. Utfallet några månader senare blev 30% lönelyft till LO och lågutbildade lärare i TCO. Högutbildade lärare i SACO fick 12%. Då tog flykten från läraryrket sin början. Vi sitter med facit.

Att sluta som lärare har aldrig varit något alternativ för mig, men min vånda har varit svår att stå ut med, så då jag äntligen fick tid, 2007, startade jag produktionen av WebMath. Mitt mål var att skapa en webbsida som via animationer visade vad den gamla skolkulturen gick ut på och att webbsidan skulle fungera direkt för eleven i klassrummet, men även som lärarhandledning där läraren dels får konkreta tips på lektionsupplägg, dels möjlighet till analys och utveckling enskilt eller tillsammans med kollegor.

4. ”Vad du än gör Westman – sluta aldrig med uppsatser!”

Vad du än gör Westman, sluta aldrig med uppsatser!…skrev eleven Anna i den årliga utvärderingen av no i åk 9. Jag hade tidigare förstått skrivprocessens betydelse för fördjupad förståelsen - att gå från en tyst kunskap till ordsatt kunskap - men hennes utvärdering blev en verklig vändpunkt för min no-undervisning och senare även matematikundervisning. Tidigare hade jag mera tänkt på hur jag själv använde språkets olika delar då jag undervisade. Nu förstod jag hur viktig det var att eleverna fick använda sitt eget språk vid inlärningen. Jag blev en kombinerad no-lärare och "läs- och skriv fröken". Och utvärderingar visade att det gav resultat.

Jag hade nämligen under tre år "tvingat" Anna och hennes klasskamrater att varje vecka som läxa lämna in en uppsats på minst 3 sidor i ett A5-häfte där de skulle besvara och analysera 3 frågor:

1. Vad har vi gjort på no-lektionerna denna vecka?

2. Vad har jag lärt mig i no denna vecka?

3. Var finns det exempel ute i samhället på det jag lärt med jag lärt i no denna vecka? 

Jag visste att Anna, från åk 7, hade kämpat med sina läs-och skrivsvårigheter för att få ihop uppsatsen, och ibland hade jag lite dåligt samvetet då jag visste att det låg flera timmars jobb bakom den inlämnade uppsatsen. I utvärderingen i åk 9 beskrev hon hur läs-och skrivproblem minskade då hon arbetade med att ordsätta vad som hänt under veckan, och att hon samtidigt upptäckte att hon kunde saker som hon inte visste att hon redan förstod. Liknande formulering använde Anders vid utvärderingen. Anders, vars pappa var sågverksägare, ägnade inte särskilt mycket kraft åt punkterna 1 och 2, men desto mer åt punkt 3, och hämtade ofta sina ”exempel ute i samhället” från verksamheten kring sågverket. Det kunde vara från virkeshanteringen, sågverket, eller från traktorn och lastbilen. Det var alltid spännande och lärorikt att varje vecka ta del av hans berättelse.

Då skrev vi på papper. Och inte bara skrev. Eleverna tecknade fantasifulla bilder som komplement till texterna, och en av dessa bilder finns med i läromedlet "Kemi modell 90" som jag skrev i mitten av 80-talet. Marias åskådliggjorde hur en syra neutraliseras av en bas genom att teckna en bild av hur en vätejon och hydroxidjon dansade med varandra och upplöstes i vatten.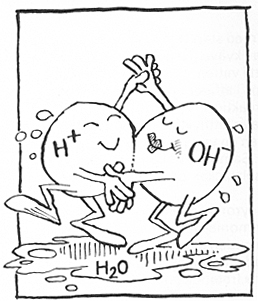

Hur tog jag då med mej erfarenheterna från uppsatserna till min matematikundervisning?

Till att börja med blev jag mera observant på hur jag bemötte eleven som frågade om hur en uppgift kunde lösas. Jag lät alltid först eleven försöka förklara vad hen inte förstod, frågade upp en eller flera gånger, ”hur menar du”, så att eleven fick tid att tänka själv. Min avsikt med frågandet var dels att försöka förstå vad eleven inte förstod, dels att eleven, under processen att förklara för mig, verkligen tänkte sig in i problemet och på så sätt satte ord på sina tankar. Ofta hände det att eleven plötsligt förstod utan min förklaring – och självförtroendet i matte växte.

I nästa steg började jag ge eleverna i läxa att med egna ord beskriva hur de förstod och tänkte sig det nya begrepp vi gått igenom, t ex ”hur tänker du dig procent”, eller ”vad är det vi egentligen gör då vi förlänger och förkortar bråk”. Läxan skulle lämnas in och förklaringen ca en A5-sida. Elevernas svar inspirerade mej att renodla metoden så att de nu fick några specifika uppgifter i läxa utan att jag först hjälpt till med en genomgång. Vid nästa lektion hade vi gemensam genomgång av läxan. Till att börja var eleverna kritiska till att jag inte hade en förklarande genomgång, men kritiken försvann efter några läxor.

Inledningsvis var jag ”sekreterare” framme vid whiteboarden, och det visade sig givetvis att det fanns olika sätt att lösa uppgifterna. Det dröjde inte länge förrän den förste eleven tog mod till sig och själv ville visa hur hen löst uppgiften och sina tankar bakom lösningen – vilket varit min avsikt. Nu tog dynamiken i undervisningen fart. Jag minns speciellt Mattias som en dag ville fram till whiteboarden och visa hur han tänkte. Jag minns hans kommentarer ”Får man tänka så här, … eller så, …. eller så här?” ”Självklart, och du har ju rätt svar” blev min kommentar. Mycket upprörd berättade han hur hans lärare på högstadiet underkänt hans sätt att tänka, vilket gjort att han trott sig vara dum i matematik Det var inga vackra omdömen han gav sin f d matematiklärare. Mattias fick självförtroende i matematik, slutade hata matematik, och tänk om det var så att hans naziztsympatier bottnade i att hans matematiktänkande helt hade nonchalerats. Vi fick en mycket god relation. Han kände tillit till mej. Jag bemötte alltid hans nazistiska kommentarer på ett sakligt sätt och bad honom förklara hur han tänkte. Kommentarerna blev allt färre med tiden och de olika naziztattributen i klädseln försvann. Då Mattias efter examen stod utanför Umeå Stadskyrka var det inte samme elev som jag två år tidigare fått som elev i matematik. En vanlig ung man som varken hatade matematik eller samhället.

I WebMath avspeglas denna metod att undervisa i matematik i att de 13 ”personerna” diskuterar sig fram till förståelse för vad matematiska begrepp är – egentligen, och att man kan tänka på olika sätt då man löser en matematikuppgift. Då man förstått återstår att öva och åter öva. Därför finns 360 testuppgifter, 164 diagnosuppgifter, 160 provuppgifter, 160 blandade uppgifter och en utvecklingslista där eleven kan bokföra sina framsteg. Facit består inte bara av ett svar, utan innehåller en kortfattad förklaring så att även facit ska vara ett inlärningstillfälle. Till diagnoserna som hör till varje kapitel finns två olika facit. Den ena är ett pdf-dokument, den andra en html-sida som är så utformad att om eleven behöver hjälp finns en länk att klicka på till varje uppgift i respektive diagnos. Länken går till de animationer som kan ge eleven hjälp.

5. Det vilar en förbannelse över matematiken!

Året är 1997. Det är mattelektion åk 2 vid Mimerskolan i Umeå. Jag har just försökt förklara för eleverna vad ett ekvationssystem är – "egentligen", och eleverna sitter och jobbar med uppgifter de fått och det är ganska tyst i klassrummet. Då hörs Jörgen mumla,  ”Nog är det väl som tusan att jag haft så otur under hela skoltiden. Alla mina tidigare mattelärare har varit så smarta att jag inte fattat vad de sagt”.  Det blev först dödstyst i klassrummet. Sedan brakade det loss i skratt och applåder, och Jörgen blev blossande röd då det gick upp för honom vad han just påstått om min intellektuella kapacitet. Jag berättade för honom att det inte går att få en bättre komplimang som lärare. Det blev en minnesvärd mattetimme. Jag tog chansen att resonera pedagogik med eleverna och berättade om den pedagogiska grundidé som ligger till grund för min undervisning.

Vad låg bakom Jörgens kommentar? Det finns en föreställning om att den som klarar matten är smart, medan den elev som har det tungt med matten får problem med självförtroendet och klassar sig själv ofta som "dum". Och Jörgen är inte ensam om sitt problem. Jag har genom åren träffat väldigt många elever och vuxna som är, eller har varit, i samma situation som Jörgen, t ex den intellektuellt mycket välmöblerad administratören i Umeå kommun som berättade att ”det där med ekvationer och x knäckte mej, så jag valde allmän kurs på högstadiet. Fortfarande får jag mer eller mindre panik om ett matematiskt problem ska lösas då andra hör på”.

Ett typiskt exempel på ”förbannelsen” är från 3 aug 2019 då Lasse Berghagen i en intervju i SVT med Lasse Kronér säger ”Matematik hade jag typ ö i”. Tänk om någon berättat för gitarristen Lasse att grekiske matematikern Pythagoras kanske var den förste gitarristen, och att han redan på 500-talet före vår tideräknings början experimenterade med strängar som han knäppte och slog på. Han upptäckte då att om en godtycklig sträng av en viss längd gav en viss ton – som vi kan kalla grundtonen – så gav halva längden av samma sträng oktaven till grundtonen. Men inte nog med det. En sträng med längden 2/3 av grundtonens gav kvinten. Då hade Lasse kanske fått intresse för matematik och sett mening med t ex bråkräkning och inte behövt känna sig dum. Kolla på "Bråkräkning och musik". Animationen är ett konkret exempel på hur jag lyckades intressera några musikaliska elever för matematik.

Jag har själv haft derivata som trauma, och kände mig verkligen "dum" på mattelektionerna. Vi y-primmade och dy/dx-ade utan att jag hade minsta aning om vad derivata var - egentligen. Jag förlöste mig ur det med hjälp av en NKI-kurs (brevkurs) under jullovet 1961.

Många gånger har vi lärare gått till klassrummet och hållit vår planerade lektion och förmedlat det vi tycker är nödvändiga kunskaper för eleverna. Men förstod eleverna, hur tänkte de om det som förklarades, vad lärde de sig, kände de sig dumma? Kanske fick vi svaret då proven rättats, och då upptäckte vi också att många elever missuppfattat eller inte förstått. För att komma till rätta med detta problem jag har haft två huvudspår. Det ena (1) är själva undervisningssituationen, det andra (2) är att synliggöra elevernas lärande och att kunna ge konstruktiv feedback.

1. All matematikundervisning borde vila på att ”Språket är bärare av all mänsklig kunskap”. Språk kan vara det talade och skrivna ordet, men även bilder, animationer, musik mm. Genom att tillsammans med eleverna resonera sig fram tillförståelse för vad de matematiska begreppen är – egentligen - skapas självförtroende i matematik, och därmed intresse och nyfikenhet för matematik. Min erfarenhet är att det är ytterst få elever som inte har förmåga att förstå matematiska begrepp. Den "dumme" måste få chansen att förstå vad de matematiska begreppen är - egentligen. Själva kärnan i all matematikundervisning är att skapa förståelse för de matematiska begreppen. Då man förstått begreppet återstår att lösa olika matematiska problem, och det kan man ju ha olika fallenhet för. Men man måste ge alla möjligheten. Jag tycker att det är näst intill en mänsklig rättighet att få chansen att förstå det matematiska begreppet, t ex att ekvationslösning egentligen inte har någonting med x att göra, eller vad derivata är i verkligheten. 

I WebMath har jag förverkligat dessa tankar genom att ”Figurerna” i WebMath visar att man kan tänka på olika sätt och resonera sig fram till förståelse, vilket är särskilt viktigt då matematiken börjar kräva abstrakt tänkande. Det är relativt enkelt att konkretisera och levandegöra grundläggande matematik, t ex additionen 3+4 med att man tar 3 kottar + 4 kottar, men då man kommer till lite mer avancerad matematik är det lätt gjort att undervisningen övergår "Gör så här så får du rätt svar", vilket inte skapar förutsättningar för nyfikenhet och intresse för vidare studier i matematik. Min ambition är att vara ett alternativ till denna härmametodik.

2. För att synliggöra elevernas lärande är det viktigt att direkt efter varje nytt moment få feedbck och på så sätt utveckla lärandet maximalt. I WebMath finns därför efter varje nytt delkapitel ett enkelt test med ca 5 uppgifter för att se om eleven förstått själva begreppet. I kapitlet bråk finns t ex, tester efter ”Vad menas med bråk?”, ”Vilket bråk är störst?”, ”Blandad form och bråkform” o s v. I slutet av kapitlet finns en diagnos med ca 25 uppgifter. Facit till alla uppgifter består inte bara av ett svar, utan innehåller en kortfattad förklaring så att även facit ska vara ett inlärningstillfälle.

Den stora utmaningen är att ge både svaga och duktiga hjälp och stimulans. Den "dumme" måste få chansen att förstå vad de matematiska begreppen är – egentligen, samtidigt som den "smarte" måste få möjlighet at ta "nästa steg" mycket snabbare än klasskamraterna för att inte bli understimulerad på mattetimmarna. Dessutom är det tyvärr så att den ”smarte” ofta av sociala skäl måste hålla inne med sin förmåga och sitt intresse för matematik för att inte bli mobbad.

På "Alla ska med" kan du läsa mer om hur jag tänkt och arbetat för att nå min målsättning.

6. Läraryrket – en kärlekshandling!

Det skakade till 11 mars 1971 och alla lärare runt om i Sverige tittade sig förskräckta om. Är det dags att lämna skeppet? Riksdagen hade antagit en tjänstepliktslag som tvingade de lockoutade lärarna tillbaka till jobbet igen. Löneuppgörelsen 9 juni 1971 efter konflikten gav LO 30% och de högutbildade lärarna i SACO 12 %. Lärarflykten tog sin början. Jag minns hur resonemangen gick.

Det verkar av den debatt som förs i media och av politiker som om den svenska skolans nedgång började i och med kommunaliseringen. Det skolhistoriska minnet verkar vara mycket kort. Sanningen är att manegen var mycket väl krattad under 18 år. LO och Socialdemokratin hade sänkt läraryrkets status så att Göran Persson utan politisk risk kunde genomföra kommunaliseringen. LO-chefen Stig Malm kunder riskfritt kalla lärare för ”värstingar” och att vi var "dåliga föredömen för elever". Vi hamnade i händerna på kommunchefer utan kunskap om hur skolan skulle skötas, och som endast lyssnade på vad forskningen och självutnämnda experter påstod. Därför lyssnade inte heller Ylva Johansson till "Beprövad erfarenhet" då hon höjde skolpengen för friskolor från 85% till 100%. Med 85% skulle friskolereformen kunnat vara hanterbar. Det är dessa 15% som skapar dagens kaos och genererar friskolors vinster. Mina ord grundar sig på mina erfarenheter, och det kanske är så att det för att kunna förstå hela nedgångsförloppet måste man ha jobbat som lärare från 60-talet och framåt. För min del anser jag att "Läraryrket är en kärlekshandling", och att det skall vara ett av samhällets bäst betalda yrken, eftersom det är ett av de svåraste yrken som finns. Jag tar ämnet matematik som exempel, bl a därför att det är i det ämnet katastrofen är tydligast.

Tidsandan från 1968: Jag skulle kunna skriva metervis om mina erfarenheter hur tidsandan från 1968 och framåt har förpestat matematikundervisningen, och om mina erfarenheter av hur lärare blivit överkörda och nonchalerade. Jag tar ett enda exempel. Det handlar om hur plötsligt arbetslag infördes i början av 80-talet. Hade lärare på högstadier bett om detta? Knappast. Och jag hörde aldrig talas om att forskningsresultat låg till grund för beslutet. Det var tidsandan som fick styra de politiska besluten, och de lärare som fortfarande hade självförtroende att protestera mobbades som "omedvetna" bakåtsträvare. Den enorma kunskapsbank som fanns hos lärarkåren nonchalerades totalt.

De revolutionära tankarna från 1968 spreds i början av 70-talet in i skolan. Att vara ”medveten” var viktigare än att ha faktiska kunskaper. Att kunna multiplikationstabellen var inte så viktigt. Det viktiga var att förstå hur den fungerade. Samtidigt klassades även betydelsen av varje enskild lärares specialkunskap ner. Arbetslagen fick till effekt att lärare var tvungna att undervisa i ämnen de inte var behöriga i. Det viktiga var att eleverna hade så få lärare som möjligt på bekostnad av kvaliteten i undervisningen! Och läromedelsförlagen hakade snabbt på. Läromedlen fick så väl uttänkta typexempel och räkneuppgifter, att eleverna enskilt kunde lösa de flesta uppgifterna i boken. Inga diskussioner pågick. Eleverna härmade och fick rätt svar - och var nöjda. Och i arbetslagen kunde "vem som helst", icke behörig i matematik, sättas in som mattelärare. Matematikläraren blev en kringvandrande handledare med allt lägre status. Och med tiden sänktes kraven i böckerna. Det som t ex 1992 ingick i särskild kurs matematik åk 9 återfanns 10 år senare i åk 1 på gymnasiet, och ibland först i åk 2, d v s en kunskapsdevalvering med 1 år. En katastrof för matematikundervisningen i Sverige.

Skolforskningens ansvar: Skolans verksamhet är lagstadgad och skolans undervisning SKALL vila på ”vetenskaplig grund och beprövad erfarenhet”. All ”Beprövad erfarenhet” bland lärare slänges överbord i de omvälvande skolreformer som kom på 80- och 90 talet. Pedagogiska forskare och självutnämnde populistiska högröstade experter tog makten. Vi sitter med facit nu. Varför övergav skolforskning lärare och tillät att pedagogiska hugslott fick slå rot i skolan? Varför lyssnade man bara till den ”medvetna” intelligentian vid universiteten som ”förstod” de stora sammanhangen, och aldrig på den enorma kunskap och erfarenhet som fanns inom lärarkåren.

Men att vara "medveten" på 70-talet innebar bl a att läxor och hårt jobb var onödigt. Redan då borde skolforskningens alla varningsklockor börjat ringa, men 68-andan rådde på universiteten, och att döma av vad jag hörde då jag bevistade en disputation hösten 2009 vid lärarutbildningen i Umeå var andan fortfarande väl förankrad.

Ur min synpunkt har det alltså gått mycket snett i pedagogiken sedan 11 mars 1971 då riksdagen fattade sitt ödesdigra beslut. Läraryrkets status skulle knäckas. Och LO och Socialdemokratin var med på tåget. Flykten från läraryrket tog sin början. Den slutgiltiga spiken slogs i då kommunaliseringen genomfördes.

Det är smärtsamt att ha upplevt den förnedring som läraryrket genomgått från att, 1965 då jag tog folkskollärarexamen, betraktas som en av samhällets viktigaste funktioner, till att då jag gick i pension 2007 anses som vilket kommunalt 8-17 jobb som helst. Efter kommunaliseringen har 8-17 tankarna smugit sig in allt kraftfullare. Den enda tillfredsställelse du ska känna är när du får ditt magra lönekuvertet för att du utfört det kommunen ålagt dig att göra. Tankar hämtade från Karl Marx. Läraren som entreprenör, och att en lärares drivkraft kan vara personlig tillfredsställelse är oönskat.

Läraryrket är ett enormt komplext och svårt yrke som kräver fallenhet för sitt utövande. För att bli antagen till lärarutbildningen 1963 krävdes förutom höga betyg, två dagar fyllda med lämplighetstester av olika slag. Läraryrket är en konstnärlig verksamhet, och för att jämföra med skådespelaryrket - vi har väldigt många föreställningar per dag, och det är alltid direktsändning, vilket tär på krafterna och kräver tid för återhämtning. Till detta kommer den självklara sanningen att läraryrket är och förblir en kärlekshandling. Denna "kärlekshandling" kan yttra sig på många olika sätt, uppfostran, tröst, att våga vara vuxen, att var bollplank, att vara väl förberedd till lektioner, våga ta sig an förändringar, stor kunskap i och intresse för de ämnen man undervisar i mm. Vad som ofta glöms bort är att själva engagemanget är i sig ett kraftfullt pedagogiskt verktyg. Ovanför entrén till varje lärarhögskola borde texten ”Läraryrket - en kärlekshandling!” lysa i eldskrift. Att läraryrket är en kärlekshandling är känt sedan tidigare. I samband med den förra verkligt stora skolreformen skriver O E L Dahm 1846 i sin bok Skolmästarkonst: "…Ty den som vid befordran till en skoltjenst tänker: Kära själ! Nu har du bröd, ät och drick och gör dig goda dagar - den är en lågsinnad menniska som aldrig fattat betydelsen af sitt kall, och som förgäter att han en gång måste avlägga räkenskap för hvarje honom anförtrodd barnasjäl".

Tjänstepliktslagen från 1971 var startskottet till skolans nedgång. Kommunaliseringen var den sista och avgörande spiken i kistan med Stig Malm och Göran Persson som ivriga tillskyndare. Till detta kom så friskolereformen. Den skulle ha kunnat vara hanterbar om beslutet på 85% ersättning till friskolorna fått ligga kvar, men så slog skolminister Ylva Johansson till med proposition 1995/96:200, som röstades igen efter en uppgörelse med Miljöpartiet, och skolpengen höjdes från 85 till 100 procent. Det är dessa 15 procent som blev startskottet för den utveckling som till idag gett oss börsnoterade koncernskolor. När ersättningen höjdes ökade vinstpotentialen. Academedia grundades 1996. Kunskapsskolan 1999. Ansvaret för utvecklingen vilar mycket tungt på Ylva Johansson.

Det finns verkligen en räkenskap att avlägga för "hvarje anförtrodd barnasjäl".

7. Från hånad och förnedrad lärare till respekterad ledare.

Det är en gnistrande kall vårvintermorgon fredag 13 maj 1966 i Malå. Klockan är 5 på morgonen. Solen lyser från en klarblå himmel. Skaren är stenhård. Ingen valla under träskidorna. Glidet är perfekt. Jag skejtar i lugn fart upp efter Malån mot Malånäs. Jag riktigt känner hur formen sitter där. Samma lätthet i kroppen som den där augustikvällen i Sundsvall 1965 då jag satte mitt personliga rekord på 1500 m. På söndag 15 maj ställs jag mot den nordiska löpareliten. Jag ska springa första sträckan för IFK Umeå i DN:s årliga stadslopp. Jag känner mig väl förberedd för uppgiften. Föga anar jag att på måndag ska jag presenteras med en stor bild på Expressen första sida, ”Överraskningsmannen Fredrik Westman”, en bild som i grunden skulle förändra min undervisningssituation vid Malå Centralskola. Jag hade mycket stora diciplinproblem. Den kaxige eleven Bosse som sett bilden släntrade in till mattelektionen försenad som vanligt, och förklarade högljutt för klassen att ”kappspringa med Fredrik är väl ingen konst”. Jag antog utmaningen. Men vi tar det från början.

Den 29 maj 1965 tog jag folkskollärarexamen vid Umeå Folkskoleseminarium. Jag hade fått lära mej en massa pedagogiska metoder hur jag skulle ta mej an undervisningen, men inte hur jag skulle handskas med disciplinproblem. Vid alla övningslektionerna på folkskoleseminariet satt alltid handledaren med, och övningsklasserna, åk 4 – 6, bestod av motiverade elever som ännu inte drabbats av pubertetens stormar.

20 augusti 1965 började jag min första tjänstgöring. Matematik och kemi vid Malå centralskola. Kemiundervisningen fungerade bra redan från början tack vare ett mycket bra samarbete med min erfarne kollega Göran Boström. Han bjöd hem mig på middag och vi gick igenom kursen och han gav mej tips om hur jag skulle kunna undervisa till att börja med. ”Så småningom kommer du att hitta din metod”. Jag hittade min metod och lyckades intressera eleverna för kemi.

Men i matematik, allmån kurs åk 8, fungerade det mycket dåligt. Jag hade enorma disciplinproblem. 4 av eleverna störde undervisningen varje lektion, och verkade njuta av situationen. De hade kommandot i klassrummet. Inte den 23-årige oerfarne matteläraren. Jag försökte förgäves på olika sätt få kontroll. Vid ett tillfälle drämde jag pekpinnen i katedern, och den gick i två bitar till elevernas förtjusning. Vid ett annat tillfälle brast det kraftfullt för mig. Jag slet upp Lars som krälade på golvet mellan och under bänkarna, bar honom ut ur klassrummet och tryckte upp honom mot tegelväggen utan för rektorsexpeditionen och vrålade, ”Jag kan inte slå ihjäl dig nu, för då får jag tjänstefel, men om jag träffar dig i kväll då är du dödens”. En förskräckt rektor Magnus kom ut och undrade. ”Jag är förbannad”, blev mitt svar och jag återvände till klassrummet. Tystnad från rektorns sida. Och inget uppföljande samtal eller någon form av support. ”Är det verkligen bara jag som har problem”? Jag lyssnade utan för klassrummen vilket gav mig tröst i eländet. Många av kollegorna hade också problem utan att berätta om det. Så var tiden då. Man stängde klassrumsdörren och pratade inte om sina problem. Egentligen var nog inte elevernas saboterande riktat mot mej personligen. De var djupt besvikna över att inte skolgången slutade efter åk 7. Den 9-åriga grundskolan infördes hösten 1965 i Malå kommun och de hade ytterligare två år att tillbringa i skolan.

Att ha genomgång av nya avsnitt var meningslöst. Det enda möjliga var att förklara enskilt, vilket gjorde att jag, p g a tidsstress, mer eller mindre lotsade eleverna förbi problemen än att förklara. Efter någon månad skaffade jag köbrickor som elever fick hämta framme vid katedern för att på så sätt försöka vara något så när rättvis i turordningen att hjälpa eleverna.

Men så kom räddningen. ”Kappspringa med Fredrik är väl ingen konst”. Jag antog utmaningen och bad Bosse byta till gympaskor, eleverna att hämta sina cyklar. Själv hämtade jag mina nya adidas tävlingsskor. Hela karavanen drog iväg söderut mot Åkroken, Jag höll en fart så att Bosse var nära sitt max. Själv var jag oberörd. Efter ca 2 km var Bosse ordentligt mör. Vi vände och jag drog på i rätt högt fart och lämnade Bosse och en del av cyklisterna bakom mej, och i sista backen upp mot skolan drog jag på för fullt och sprang ifrån de som fortfarande hängde med.

Vi återgick till mattelektionen och efter en stund smög en skamsen Bosse in. Från den stunden var jag den respekterade ledaren i klassen. Inga disciplinproblem. Jag var plötsligt den självklare och respekterade ledaren i klassrummet. Det var lugnt och stilla på lektionerna och jag kunde börja använda de metodiska tips jag fått med mej från folkskoleseminariet. Jag berättade aldrig om denna lektion för mina kollegor.

I nästa inlägg ska berätta om vilken lärdom jag drog av denna minnesvärda 80-minuterslektion i matematik?

8. Läraren som ledare och förebild.

Vad drog jag då för lärdom av den minnesvärda 80-minuterslektionen i matematik? Det stod klart för mig att varje gång jag mötte en ny klass, var det nödvändigt att på något sätt ge alla elever en känsla av trygghet. De första minuterna kunde vara avgörande för min relation till klassen under våra år tillsammans. Det var jag som skulle framstå som ledaren och förebilden i klassrummet, inte någon eller några av eleverna. Jag skulle vara en auktoritet i deras ögon, dock utan att vara auktoritär.

Jag provade mej fram på olika sätt. Till att börja med slopade jag sega upprop, som bl a kunde ge klassens clown möjlighet att spela ut sitt register och ta kommandot. I stället hälsade jag dem välkomna och presenterade vem jag var. Därefter under några minuter hur jag skulle lägga upp lektionerna, och vad vi skulle hinna med under läsåret, och vilken insats som jag förväntade mej av eleverna. Jag lovade att jag alltid skulle vara väl förberedd till varje lektion, vilket gjorde att jag krävde att eleverna alltid skulle vara i tid till lektionerna. Eftersom jag lagt ner mycket jobb på att kunna vara till hjälp, var det en personlig förolämpning mot mej att inte vara i tid. I slutet av första lektionen gjorde jag en klassrumskarta med elevernas namn och bad eleverna att minnas sin plats till nästa lektion. Jag pluggade in kartan till nästa lektionstillfälle så att jag skulle kunna tilltala dem med deras namn och på så sätt ta bort all anonymitet och ge varje elev känslan av att vara sedd. Metoden fungerade rätt bra.

Så småningom utvecklade jag introduktionen genom att berätta om min pedagogiska idé, bl a att jag ville ha igång ett samtal vid varje lektion. För att det skulle fungera krävdes ett tillåtande klimat i klassrummet, d v s den elev som inte förstod skulle känna sig trygg att våga fråga, även upprepat, tills hen förstått. Detta utan att någon annan elev försökte glänsa och nedvärdera eleven som inte förstod. Jag berättade för eleverna att om någon av dem inte förstod så var det i regel fler som inte förstod. För att metoden skulle fungera krävdes det av mej att vara mycket tydlig då ”glänsaren” slog till första gången. Jag var ledaren som bestämde. Jag minns hur den mycket matematikbegåvade Göran viskade ”sopa” vid ett tillfälle. Jag tog chansen och förklarade för honom skillnaden mellan matematikkunskaper och människovärde. Visserligen var han duktig i matematik, men för den skull hade han inte mera människovärde än eleven som frågade. Och absolut inga rättigheter att förtrycka andra elever.

I nästa utvecklingssteg lärde jag mej elevernas namn och utseende med hjälp av skolfoton. Då jag träffade klassen första gången inledde jag lektionen som om det var en vanlig lektion. Inget upprop. Efter en stund dök alltid frågan upp, ofta ställd av klassens informelle ledare. ”Hur kan du veta vad vi heter?” ”Säpo” brukade jag svara, och kunde fortsätta med att jag även kände ”X” som också kom från samma by den informelle ledaren, eller till och med var syskon till frågeställaren. Vad jag ville uppnå var att alla skulle känna sig identifierade och sedda och att jag faktiskt hade lagt ner jobb med att lära allas namn. ”Han verkar ju bry sig”. Dessa första minuter grundlade relationen under resten av den tid vi skulle ha tillsammans.

Det första föräldramötet var också ett mycket viktigt tillfälle att nå ut med hur jag ville ha det i klassrummet. Allteftersom förändrade jag karaktären på mötena. Efter genomgång av sedvanliga praktiska detaljer, scheman mm, förklarade jag kort min pedagogiska idé, och avslutade med att be föräldrar om hjälp med att kunna genomföra den. ”Jag vill att era barn är mätta, har sovit tillräckligt och är någorlunda harmoniska då de kommer till skolan – då har jag möjlighet att göra ett bra jobb”. Ett stort, enkelt, tydligt och egentligen ganska självklart krav, ett av föräldrar mycket uppskattat krav.

Det som verkligen bekymrar mig är högröstade, av skattemedel mycket välbetalda, föreläsares budskap om att läraren ska vara en skojsig typ, en rolig vuxenpolare och kompis med eleverna. Jag har för min del aldrig strävat efter att vara kompis med mina elever eller försökt göra mig populär. Det viktiga för mej har varit att våga vara vuxen, med allt vad det innebär. Hur kan det vara möjligt att de som bär ansvar för den svenska skolan låter högröstade, karismatiska ”frälsare” få genomslag för sina populistiska idéer och leda skolan in på villovägar? 

För min del - då jag hör och läser om olika populistiska infall - brukar jag tänka på vad Torgny Lindgren skriver i ”Dorés bibel”: "Strängt taget är det ju ett hantverk jag ägnat mig åt. Och hantverket är alltid mera krävande än det rena hämningslösa tänkandet….”. Läraryrket är ett krävande hantverk fjärran från hämningslösa populistiska idéer.

9. Är procent så här enkelt?

Året är 1994. Det är matematiklektion åk 1 gymnasiet vid Mimerskolan i Umeå. Det är första lektionstillfället om procent. Elevgruppen består av elever som går linjerna media och estetik, och många är musiker. Det visar sig att procentbegreppet är väldigt luddigt för många. På min fråga vad procent är blir svaren t ex ”Någonting med 100”, ”Man ska multiplicera med 0,01 om det är en procent”.

1994 fanns inga videoprojektorer. Vi använde OH-projektorer med genomskinlig skrivfilm, transparenter som de kallades. Målet med nästa lektionstillfälle är att alla elever ska förstå vad begreppet procent är och hur bråk och procent hänger ihop. För att nå målet anpassar jag lektionen till musikelevernas värld och kopierar noterna ur ”Blinka lilla stjärna där” och ”Mors lilla Olle” till två transparenter. Lektionen inleds med att jag sjunger ”Blinka lilla stjärna där”, nu med texten 25%, 25%, 25%, 25%,25%, 25%, och 50% …, och pekar samtidigt på varje not då jag sjunger. (De svarta noterna på bilden är fjärdedelsnoter, 25%, och de vita är halvnoter, 50%.)

Vi resonerar omkring bilden och det visar sig att de flesta eleverna har klart för sig att 4 st fjärdedelsnoter ger en hel takt, d v s 100%, och en halvnot är en halv takt, d v s 50%. 25% är alltså en fjärdedel och 50% en halv, och man kan skriva notvärdena i både bråk- och decimalform.

Jag fortsätter med nästa transparent och sjunger ”Mors lilla Olle” och pekar samtidigt på varje not. (Noterna med en flagga är åttondelsnoter, 12,5%)

Här förklarar jag på sambandet mellan procent och bråk som bilden visar. Det visar sig också att krumeluren i slutet på andra takten måste vara en fjärdedel för att få en hel takt, d v s 100%. De flesta eleverna känner redan till symbolen för en fjärdedels paus. Resten av lektionen ägnar vi åt att resonera om hur bråk och procent hänger ihop. Eleverna får själva föreslå olika exempel.

Jag berättar också för eleverna att den grekiske matematikern Pythagoras kanske var den förste gitarristen, och att han redan för ca 2500 är sedan experimenterade med strängar som han knäppte på. Han upptäckte då att om en sträng av en viss längd ger en viss ton, grundton, så ger halva längden av samma sträng oktaven till grundtonen. En sträng med längden 2/3 av grundtonens längd ger kvinten. Begreppen grundton, oktav och kvint är kända av de flesta eleverna.

Vid nästa lektion kommer en glad Frida fram till mej. ”Jag klarade alla läxuppgifterna. Inte visste jag att procent är så här enkelt”. Självförtroendet lyser i hennes ögon.

Genom att tillsammans med eleverna resonera sig fram tillförståelse för vad de matematiska begreppen är – egentligen - skapas självförtroende i matematik, och därmed intresse och nyfikenhet för matematik. Min erfarenhet är att det är ytterst få elever som inte har förmåga att förstå matematiska begrepp. Det viktiga, och det mycket svåra, är att nå eleven där hen är i sitt tänkande och sin vardag. I den här lektionen passade det med musik för de flesta av eleverna och jag upplevde att även de som inte hade musik i sin vardag hängde med i resonemangen och förstod hur procent och bråk hänger ihop. Och vem kunde ha trott att bråkräkning har sin grund i musik.

I WebMath återfinns denna lektion i animationerna "Bråkräkning och musik" och "Olivias procentlåt"

10. Varför har ingen hällt vatten?!

"Varför har ingen hällt vatten tidigare? Är volym så här djävla enkelt"?

Året är 1995. Matematiklektion om volym åk 1 på medieprogrammet på Mimerskolan, Umeå. Anna som sitter längst fram lite till höger är mycket upprörd. "Jag aldrig förstått vad volym är, bara att man får fram svaret genom att multiplicera längd, bredd och höjd med varandra". Det visade sig sedan att Anna hade samma problem med procent, ekvationer m m. Ingen hade förklarat för henne vad själva begreppet stod för, t ex att procent är ett fiffigt sätt att jämföra och hur bråkräkning och procent hänger ihop. "I procent ska man ibland dela med 100 eller multiplicera med 0,1 eller 0,01". "Och det där med att räkna med x" hade hon aldrig förstått. Efter Annas utbrott visade det sig att hon minsann inte var ensam om att ha problemen med begreppsförståelse i matematik. Vi hade ett mycket givande och lärorikt läsår, både för mig som lärare och för eleverna.

Jag använde dessa volymmodeller och hällde vatten för att visa vad begreppet volym står för. Elever blir ofta förvånade att det ryms en hel liter i kubikdecimetern, d v s en liter = kubikdecimeter. Lika förvånade blir de av att det ryms 3 pyramider i en kub om pyramiden har lika stor basyta och höjd som kuben. Och på samma sätt med konens volym. Efter hällandet av vatten är det lätt för eleverna att förstå varför formeln för pyramidens och konens volym har en trea i nämnaren.

Återigen - självförtroende i matematik, och därmed intresse och nyfikenhet för matematik, skapas genom att eleverna får förståelse för vad de matematiska begreppen är – egentligen. I detta exempel genom hälla vatten och tillsammans med eleverna resonera sig fram till förståelse för vad det matematiska begreppet volym är.