Facit, Procentkassa
Ge inte upp om ditt svar inte stämmer med facit. Du kan ha tänkt helt rätt, men bara räknat fel. Prova en gång till. Om ditt svar ändå inte stämmer med facit, kan du gå till "Sök animation eller rubrik" för att hitta en animation som ger förklaring, eller berätta för din lärare hur du tänkt, och be om hjälp. Du kan vara inne på rätt spår och behöver bara en liten knuff framåt. Och om du inte förstår förklaringen, ställ följdfrågor ända tills du förstått. Då kommer självförtroendet. Lämna aldrig en uppgift utan att du förstått.
Uppgift 1 - Procent, bråkform, decimalform.
Man kan antingen förlänga bråken så att nämnaren blir 100, eller räkna division, d v s täljaren delat med nämnare. 2/3 går inte jämnt upp, utan måste avrundas.

Uppgift 2 - Procent och procentenheter.
a) Minskningen var 0,6 procentenheter.
b) Minskningen var 10%.

Uppgift 3 - Procent och hästaffärer.
a)

b)
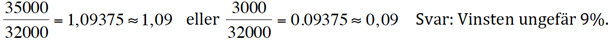
Uppgift 4 - Procent och rabatt.
a) 25% = 660 kr. Då blir det ursprungliga priset, d v s 100% fyra gånger så mycket, alltså 2640 kr
Man kan också använda ekvationslösning. Antag att det ursprungliga priset är x kr.

b) Olga ska betala 2640 kr - 660 kr = 1980 kr.
Uppgift 5 - Procentuell höjning/sänkning.
En höjning med 14% kan skrivas 1,14, d v s 100% + 14%, och en sänkning med 14% kan skrivas 0,86, d v s 100% - 14%.

Uppgift 6 - Procent och moms.
Då man lägger på 25% moms och vill veta priset inklusive moms multiplicerar man med 1,25. Då man vet priset inklusive 25% moms får man priset exklusive moms genom att antingen multiplicera inklusive-priset med 0,8, eller dela med 1,25. Svar: Varan kostar 80 kr exklusive moms.
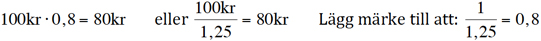
Uppgift 7 - Procent, konsumentprisindex.
Konsumentprisindex ökade från 132,6 till 153,8. Man ska alltså jämföra 153,8 med 132,6 för att få den procentuella höjningen.

Uppgift 8 - Procent och ränta.
Ett ränteår har 360 dagar. Räntetiden här blir alltså 45 delat med 360.
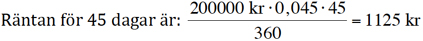
Uppgift 9 - Procent och ränta på ränta.
3% ränta betyder att kapitalet ökar med 103% varje år, d v s man ska multiplicera med 1,03 fem år i följd. Förändringsfaktorn är 1,03.

Uppgift 10 - Procent, ränta och skatt.
Man gör skatteavdraget (30%) genom att multiplicera räntan med 0,7. Räntetiden under 1993 är ett halvår, d v s 0,5 år.

Uppgift 11 - Procent och aktier.
Svar: Aktiens värde har stigit med ungefär 24%.
Då aktien stiger med 12% får man aktievärdet efter ett år genom att multiplicera med 1,12. De följande åren multiplicerar man i tur och ordning med 1,15 respektive 1,20. Då aktievärdet sjunker med 20% får man aktievärdet genom att multiplicera med 0,80. Man kan också anta att aktievärdet är x kr och räkna som alternativ 2 visar. Vid slututräkningen (rad 3) förkortar man med x.
Alternativ 1:

Alternativ 2:

Uppgift 12 - Procent, ränta, amortering.
Med rak amortering menas att man amorterar lika stort belopp vid varje amorteringstillfälle.

Svar: Räntekostnaden under första året är 3465 kr.
Uppgift 13 - Procent och snabblån.
Månadsräntan motsvarar 360 kr. Räntesatsen för en månad blir då 360 kr delat 1500 kr. Årsräntesatsen, d v s den verkliga räntesatsen blir 12 gånger större.

Svar: Den verkliga räntesatsen för snabblånet var 288%.
Uppgift 14 - Procent, fart, tid, sträcka.
a) Svar: Kl 9.45 + 4 h 15 min = kl 14.00. Man är framme kl 14.00.
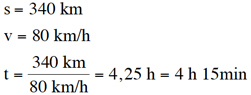
b) Då man är framme 13.09 har resan tagit 3h 24 min = 3,4 h. Fartökningen är 20 km/h. Svar: Höjning av medelfarten är 25%.

c) Svar: Teoretiskt är det möjligt, men knappast i praktiken. Om man håller fartgränsen 110 km/h är man framme ca kl 13.00, d v s det finns bara tid för sammanlagt 9 minuters paus under hela resan, och då får det inte ha inträffat något som tillfälligt sänkt farten.
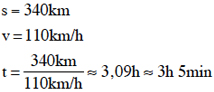
Uppgift 15 - Procent och alkohol.
a) Svar: Burken innehåller 1,75 cl 100%-ig alkohol.

b) Svar: Burkens alkoholmängd motsvarar 4,375 cl 40%-ig alkohol.
Antag att burkens alkoholmängd motsvarar x cl 40%-ig alkohol.

Uppgift 16 - Procent och Pythagoras sats.
Den egyptiska triangelns sidor är 3 cm, 4 cm och 5 cm. En egyptisk triangel är en rätvinklig triangel.


a) Svar: Den egyptiska triangelns area utgör ca 31% av cirkelns area.

b) Antag att cirkelns diameter är 5x cm.


Uppgift 17 - Procent, geometri, algebra.
Svar: Cirkelns omkrets är ungefär 21% mindre än än kvadratens omkrets.


Uppgift 18 - Procent, geometri, algebra.
Svar: Cirkelns area är ungefär 57% större än kvadratens area.
Antag att kvadratens sida är a.

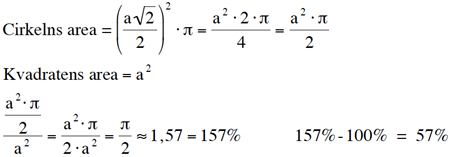
Uppgift 19 - Procent och ekvationer.
Svar: Tröjan kostade 145 kr före prissänkningarna.
Antag att priset på tröjan från början var x kr.

Uppgift 20 - Procent och statistik.
Svar: 25% av procent av eleverna såg 4 nyhetsprogram under en vecka.
Totalt var 20 elever tillfrågade. 5 elever såg 4 nyhetsprogram under en vecka.

Man kan antingen förlänga bråken så att nämnaren blir 100, eller räkna division, d v s täljaren delat med nämnare. 2/3 går inte jämnt upp, utan måste avrundas.

a) Minskningen var 0,6 procentenheter.
b) Minskningen var 10%.

a)

b)
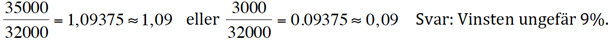
a) 25% = 660 kr. Då blir det ursprungliga priset, d v s 100% fyra gånger så mycket, alltså 2640 kr
Man kan också använda ekvationslösning. Antag att det ursprungliga priset är x kr.

b) Olga ska betala 2640 kr - 660 kr = 1980 kr.
En höjning med 14% kan skrivas 1,14, d v s 100% + 14%, och en sänkning med 14% kan skrivas 0,86, d v s 100% - 14%.

Då man lägger på 25% moms och vill veta priset inklusive moms multiplicerar man med 1,25. Då man vet priset inklusive 25% moms får man priset exklusive moms genom att antingen multiplicera inklusive-priset med 0,8, eller dela med 1,25. Svar: Varan kostar 80 kr exklusive moms.
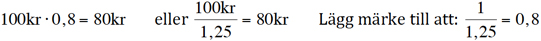
Konsumentprisindex ökade från 132,6 till 153,8. Man ska alltså jämföra 153,8 med 132,6 för att få den procentuella höjningen.

Ett ränteår har 360 dagar. Räntetiden här blir alltså 45 delat med 360.
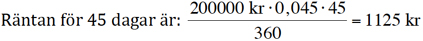
3% ränta betyder att kapitalet ökar med 103% varje år, d v s man ska multiplicera med 1,03 fem år i följd. Förändringsfaktorn är 1,03.

Man gör skatteavdraget (30%) genom att multiplicera räntan med 0,7. Räntetiden under 1993 är ett halvår, d v s 0,5 år.

Svar: Aktiens värde har stigit med ungefär 24%.
Då aktien stiger med 12% får man aktievärdet efter ett år genom att multiplicera med 1,12. De följande åren multiplicerar man i tur och ordning med 1,15 respektive 1,20. Då aktievärdet sjunker med 20% får man aktievärdet genom att multiplicera med 0,80. Man kan också anta att aktievärdet är x kr och räkna som alternativ 2 visar. Vid slututräkningen (rad 3) förkortar man med x.
Alternativ 1:

Alternativ 2:

Med rak amortering menas att man amorterar lika stort belopp vid varje amorteringstillfälle.

Svar: Räntekostnaden under första året är 3465 kr.
Månadsräntan motsvarar 360 kr. Räntesatsen för en månad blir då 360 kr delat 1500 kr. Årsräntesatsen, d v s den verkliga räntesatsen blir 12 gånger större.

Svar: Den verkliga räntesatsen för snabblånet var 288%.
a) Svar: Kl 9.45 + 4 h 15 min = kl 14.00. Man är framme kl 14.00.
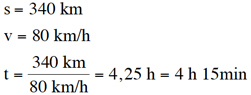
b) Då man är framme 13.09 har resan tagit 3h 24 min = 3,4 h. Fartökningen är 20 km/h. Svar: Höjning av medelfarten är 25%.

c) Svar: Teoretiskt är det möjligt, men knappast i praktiken. Om man håller fartgränsen 110 km/h är man framme ca kl 13.00, d v s det finns bara tid för sammanlagt 9 minuters paus under hela resan, och då får det inte ha inträffat något som tillfälligt sänkt farten.
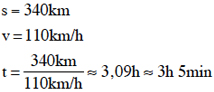
a) Svar: Burken innehåller 1,75 cl 100%-ig alkohol.

b) Svar: Burkens alkoholmängd motsvarar 4,375 cl 40%-ig alkohol.
Antag att burkens alkoholmängd motsvarar x cl 40%-ig alkohol.

Den egyptiska triangelns sidor är 3 cm, 4 cm och 5 cm. En egyptisk triangel är en rätvinklig triangel.


a) Svar: Den egyptiska triangelns area utgör ca 31% av cirkelns area.

b) Antag att cirkelns diameter är 5x cm.


Svar: Cirkelns omkrets är ungefär 21% mindre än än kvadratens omkrets.


Svar: Cirkelns area är ungefär 57% större än kvadratens area.
Antag att kvadratens sida är a.

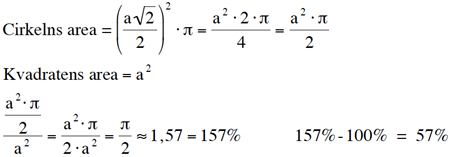
Svar: Tröjan kostade 145 kr före prissänkningarna.
Antag att priset på tröjan från början var x kr.

Svar: 25% av procent av eleverna såg 4 nyhetsprogram under en vecka.
Totalt var 20 elever tillfrågade. 5 elever såg 4 nyhetsprogram under en vecka.
