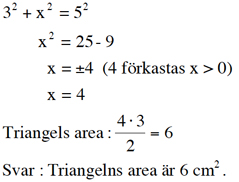Facit, Geometrikassa
Ge inte upp om ditt svar inte stämmer med facit. Du kan ha tänkt helt rätt, men bara räknat fel. Prova en gång till. Om ditt svar ändå inte stämmer med facit, kan du gå till "Sök animation eller rubrik" för att hitta en animation som ger förklaring, eller berätta för din lärare hur du tänkt, och be om hjälp. Du kan vara inne på rätt spår och behöver bara en liten knuff framåt. Och om du inte förstår förklaringen, ställ följdfrågor ända tills du förstått. Då kommer självförtroendet. Lämna aldrig en uppgift utan att du förstått.
Uppgift 1 - Geometri, kvadrat, kub.
Uppgift 2 - Geometri, cirkel.
Uppgift 3 - Geometri, cirkel.
Uppgift 4 - Geometri, procent.


Eftersom alla tre vinklarna är 60 grader är triangeln liksidig med sidorna 6 cm. Höjen mot en sida delar sidan i två lika stora delar. Pythagoras sats ger:
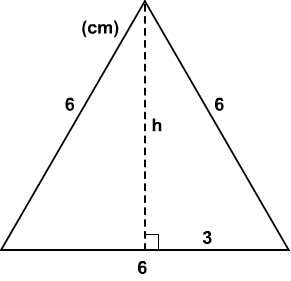
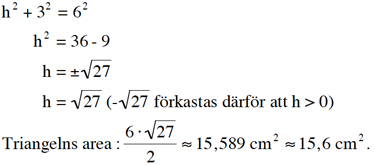
Man kan givetvis också direkt använda formeln för höjden i en liksidig triangel.

a) 45 min = 3/4 h = 0,75 h.

b) På kartan blir starens flygsträcka 100000 gånger kortare än i verkligheten, d v s men delar flygsträckan med 100000.

a) Vinkelsumman i en fyrhörning är 360 grader. Antagande enligt figur.


b) Antagande enligt figur.

Eftersom triangeln ABC är likbent är basvinklarna A och C lika stora, 70 grader. DC är bisektris till vinkeln C. Alltså är vinkeln DCA 35 grader. Eftersom vinkelsumman i en triangel är 180 grader är vinkeln x = 75 grader.
Svar: Vinkeln x är 75 grader.
a) Antagande enligt figur.
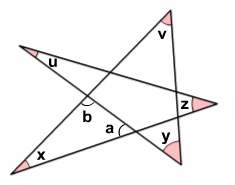
Yttervinkelsatsen ger:
a = u + z
b = y + v
x + a + b = 180 grader (Vinkelsumman i en triangel).
Alltså är x + u + z + y + v = 180 grader.
b) Triangeln ABC är likformig med triangeln DBE. Likformighet ger följande två ekvationer:

a) Vinkeln x = 30 grader. (Likbent triangel). Medelpunktsvinkeln är då 120 grader, vilket i sin tur ger randvinkeln y = 60 grader.
b) Antagande se figur.

Vinkeln y = 80 grader (Medelpunktsvinkel).
Vinkeln z = 50 grader (Triangeln BDC är likbent. Vinkelsumman i en triangel).
Vinkeln x + z = 70 grader (Triangeln ABC är likbent. Vinkelsumman i en triangel).
Svar: Vinkeln x = 20 grader.
Vinkeln ABC är 90 grader, därför att vinkeln mellan en radie och en tangent till cirkeln i tangeringspunkten är 90 grader. Sträckan AC är 5 cm. Då är triangeln ABC en Egyptisk triangel, och sidan BC är 4 cm. Man kan även beräkna BC med Pythagoras sats. Antag att BC är x cm.
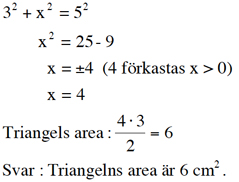
Längdskalan är 3:1. Areaskalan = kvadraten på längdskalan, d v s 9:1. Alltså är arean av den stora triangeln 90 kvadratcentimeter. Detta ger ekvationen:















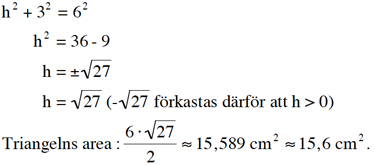


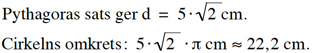








 Eftersom triangeln ABC är likbent är basvinklarna A och C lika stora, 70 grader. DC är bisektris till vinkeln C. Alltså är vinkeln DCA 35 grader. Eftersom vinkelsumman i en triangel är 180 grader är vinkeln x = 75 grader.
Eftersom triangeln ABC är likbent är basvinklarna A och C lika stora, 70 grader. DC är bisektris till vinkeln C. Alltså är vinkeln DCA 35 grader. Eftersom vinkelsumman i en triangel är 180 grader är vinkeln x = 75 grader.